Công thức tính Cấp số cộng và cách giải các dạng bài tập (2024) chi tiết nhất

Công thức cấp cho số nằm trong - Toán lớp 11

Bạn đang xem: Công thức tính Cấp số cộng và cách giải các dạng bài tập (2024) chi tiết nhất

I. Lý thuyết Cấp số cộng

1) Định nghĩa

(u_n) là cấp cho số nằm trong Khi $u_{n+1}=u_n+d,n\in {\mathbb{N}}^{*}$ (d gọi là công sai)

Nhận xét:

- Cấp số nằm trong (u_n) là 1 trong những sản phẩm số tăng Khi và chỉ Khi công sai d > 0.

- Cấp số nằm trong (u_n) là 1 trong những sản phẩm số hạn chế Khi và chỉ Khi công sai d < 0.

- điều đặc biệt, Khi d = 0 thì cấp cho số nằm trong là 1 trong những sản phẩm số ko thay đổi (tất cả những số hạng đều bởi nhau).

2) Số hạng tổng quát của cấp cho số nằm trong (u_n) được xác lập bởi công thức:

u_n = u₁ + (n – 1)d với $n\in {\mathbb{N}}^{*},n\ge 2$.

3) Tính chất

Ba số hạng là phụ thân số hạng tiếp tục của cấp cho số nằm trong Khi và chỉ Khi $u_k=\frac{u_{k-1}+u_{k+1}}{2}$.

II. Công thức cấp cho số cộng

- Công thức tính công sai: d = u_n+1 – u_n với $n\in {\mathbb{N}}^{*}$.

- Công thức tìm hiểu số hạng tổng quát: u_n = u₁ + (n – 1)d với $n\in {\mathbb{N}}^{*},n\ge 2$.

- Tính hóa học của 3 số hạng $u_{k-1},u_k,u_{k+1}\left(k\ge 2\right)$ tiếp tục của cấp cho số cộng: $u_k=\frac{u_{k-1}+u_{k+1}}{2}$.

- Tổng n số hạng thứ nhất của cấp cho số cộng: $S_n=\frac{n\left(u_1+u_n\right)}{2}=\frac{n\left[2u_1+\left(n-1\right)d\right]}{2}$.

III. Ví dụ minh họa

Ví dụ 1: Cho cấp cho số nằm trong (u_n) thỏa mãn: $\left\{\begin{array}{c}{u}_2-u_3+u_5=10\\ u_4+u_6=26\end{array}\right.$

a) Xác tấp tểnh công sai và số hạng thứ nhất của cấp cho số nằm trong.

b) Xác tấp tểnh công thức số hạng tổng quát tháo của cấp cho số nằm trong.

c) Tính số hạng loại 100 của cấp cho số nằm trong.

d) Tính tổng 15 số hạng thứ nhất của cấp cho số nằm trong.

Lời giải

a) Gọi d là công sai của cấp cho số nằm trong, tớ có:

$\begin{array}{l}\left\{\begin{array}{c}{u}_2-u_3+u_5=10\\ u_4+u_6=26\end{array}\right.\\ \iff \left\{\begin{array}{l}(u_1+d)-(u_1+2d)+(u_1+4d)=10\\ (u_1+3d)+(u_1+5d)=26\end{array}\right.\\ \iff \left\{\begin{array}{l}{u}_1+3d=10\\ u_1+4d=13\end{array}\right.\iff \left\{\begin{array}{l}{u}_1=1\\ d=3\end{array}\right.\end{array}$

Vậy công sai d = 3 và số hạng thứ nhất u₁ = 1.

b) Số hạng tổng quát: u_n = u₁ + (n – 1)d = 1 + (n – 1).3 = 3n – 2.

c) Số hạng loại 100 là: u₁₀₀ = 3.100 – 2 = 298.

d) Tổng 15 số hạng đầu tiên:

$S_{15}=\frac{n\left[2u_1+\left(n-1\right)d\right]}{2}=\frac{15.\left(2.1+14.3\right)}{2}=330$

Ví dụ 2: Cho cấp cho số nằm trong (u_n) thỏa mãn: u_n = 2n – 3.

a) Xác tấp tểnh công sai của cấp cho số nằm trong.

b) Số 393 là số hạng loại từng nào của cấp cho số nằm trong.

c) Tính S = u₁ + u₃ + u₅ + … + u_2021.

Lời giải

a) Ta có: u_{n + 1} = 2(n + 1) – 3 = 2n – 1

Xem thêm: Người sinh năm 2008 mệnh gì? Hợp với tuổi nào? Tính cách và sự nghiệp của người sinh năm này

Công sai của cấp cho số cộng: d = u_n+1 – u_n = (2n – 1) – (2n – 3) = 2

b) Gọi số hạng loại k của cấp cho số nằm trong là 393, tớ sở hữu u_k = 393.

Khi đó: 2k – 3 = 393. Suy rời khỏi k = 198.

Vậy số 393 là số hạng loại 198 của cấp cho số nằm trong.

c) Ta có: u₁ = 2 . 1 – 3 = – 1

Dãy số là (v_n): u₁; u₃; u₅; … u₂₀₂₁ là cấp cho số cùng theo với số hạng thứ nhất là u₁ = – 1 và công sai d’ = u₃ – u₁ = 2d = 4

Dãy (v_n) có: (2021 – 1) : 2 + 1 = 1011 số hạng

Vậy tổng $S=u_1+u_3+u_5+\dots +u_{2021}$$=\frac{1011.\left(2.\left(-1\right)+1010.4\right)}{2}=2041209$.

IV. Bài tập

Bài 1: Cho cấp cho số nằm trong (u_n) sở hữu u₁ = 1 và d = – 3.

a) Xác tấp tểnh số hạng tổng quát tháo của cấp cho số cộng

b) Tìm số hạng loại 2021 của cấp cho số cộng

c) Số – 488 là số hạng loại từng nào của cấp cho số nằm trong.

Lời giải

a) Số hạng tổng quát:

u_n = u₁ + (n – 1)d = 1 + (n – 1).(– 3) = – 3n + 4.

b) Số hạng loại 2021 của cấp cho số cộng:

u₂₀₂₁ = – 3.2021 + 4 = – 6059.

c) Gọi số hạng loại k là số – 488, tớ có: u_k = – 3k + 4 = – 488. Suy rời khỏi k = 164.

Vậy số – 488 là số hạng loại 164.

Bài 2: Cho cấp cho số nằm trong (u_n) vừa lòng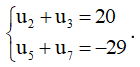

a) Tìm u₁; d?

b) Xác tấp tểnh số hạng tổng quát tháo của cấp cho số nằm trong.

c) Số –1372,5 là số hạng loại từng nào của cấp cho số nằm trong.

Lời giải

a) Ta có:

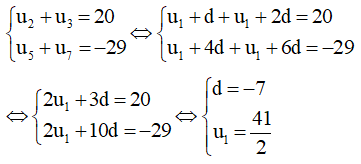
Vậy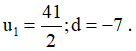

b) Số hạng tổng quát:

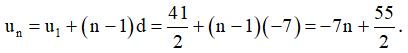
c) Gọi số hạng loại k là số – 1372,5, tớ có: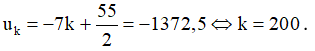

Vậy số – 1372,5 là số hạng loại 200.

Xem thêm thắt tổ hợp công thức môn Toán lớp 9 không thiếu và cụ thể khác:

Công thức tính công sai của cấp cho số cộng

Công thức tìm hiểu số hạng tổng quát tháo của cấp cho số cộng

Xem thêm: Nam, nữ Bính Thìn 1976 mệnh gì? Hợp màu nào, công việc gì?

Công thức tính tổng n số hạng đầu của cấp cho số cộng

Công thức cấp cho số nhân

Công thức tính công bội của cấp cho số nhân