Tailieumoi.vn van ra mắt cho tới những quý thầy cô, những em học viên đang được nhập quy trình ôn tập dượt cỗ bài bác tập dượt Góc thân thiết đường thẳng liền mạch và mặt mày phẳng Toán lớp 12, tư liệu bao hàm 12 trang, tuyển chọn lựa chọn những bài bác tập dượt Góc thân thiết đường thẳng liền mạch và mặt mày phẳng lặng rất đầy đủ lý thuyết, cách thức giải cụ thể và bài bác tập dượt sở hữu tiếng giải, chung những em học viên đạt thêm tư liệu tìm hiểu thêm nhập quy trình ôn tập dượt, gia tăng kỹ năng và kiến thức và sẵn sàng mang lại kì thi đua chất lượng tốt nghiệp trung học phổ thông môn Toán tiếp đây. Chúc những em học viên ôn tập dượt thiệt hiệu suất cao và đạt được sản phẩm như chờ mong.
Mời những quý thầy cô và những em học viên nằm trong tìm hiểu thêm và chuyên chở về cụ thể tư liệu bên dưới đây:
Bạn đang xem: Góc giữa đường thẳng và mặt phẳng là gì? Cách xác định và bài tập
1. Định nghĩa
Góc thân thiết đường thẳng liền mạch và mặt mày phẳng lặng là góc thân thiết đường thẳng liền mạch và hình chiếu vuông góc của chính nó lên bên trên mặt mày phẳng lặng.
Nếu đường thẳng liền mạch a vuông góc với mặt mày phẳng lặng (P) thì tớ thưa góc thân thiết đường thẳng liền mạch a và mặt mày phẳng lặng (P) vày 90 chừng. (hình 1).
Nếu đường thẳng liền mạch a ko vuông góc với mặt mày phẳng lặng (P) thì góc thân thiết đường thẳng liền mạch a và mặt mày phẳng lặng (P) là góc thân thiết đường thẳng liền mạch a và hình chiếu a' của chính nó lên trên bề mặt phẳng lặng (P) (hình 2).
Chú ý: Góc thân thiết đường thẳng liền mạch và mặt mày phẳng lặng ko vượt lên trước vượt .
2. Phương pháp giải
Sử dụng khái niệm góc thân thiết đường thẳng liền mạch và mặt mày phẳng lặng.
Tìm giao phó điểm
Tìm một điểm A tùy ý bên trên đường thẳng liền mạch a và xác đánh giá chiếu vuông góc H của A bên trên mặt mày phẳng lặng (P). Khi tê liệt, là đường thẳng liền mạch trải qua nhị điểm A và M. Ta sở hữu
(trong tê liệt là khoảng cách kể từ điểm A cho tới mặt mày phẳng lặng (P)).
3. Bài tập dượt ví dụ
Gọi H là hình chiếu vuông góc của S bên trên mặt mày phẳng lặng lòng (ABC).
Như vậy HA là hình chiếu vuông góc của SA bên trên (ABC).
Vậy
Ví dụ 1: Cho hình chóp S.ABC sở hữu lòng ABC là tam giác vuông bên trên B, sở hữu AB = a. sành , SB tạo nên với lòng một góc 600 và M là trung điểm của BC.
a) Tính cosin góc thân thiết SC và mặt mày phẳng lặng (ABC).
b) Tính cosin góc thân thiết SM và mặt mày phẳng lặng (ABC).
a) Do
Do đó
Ta có:
Khi đó:
b) Do
Ta có:
Khi đó
Ví dụ 2: Cho hình chóp S.ABCD, lòng là hình chữ nhật sở hữu \[AB = 2a;AD = a\]. Tam giác (SAB) đều và nằm trong mặt mày phẳng lặng vuông góc với lòng.
a) Tính góc thân thiết SB, SC và mặt mày phẳng lặng (ABCD).
b) Gọi I là trung điểm của BC. Tính tan góc thân thiết SI và mặt mày phẳng lặng (ABCD).
Lời giải
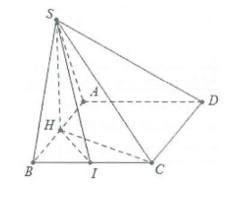
a) Gọi H là trung điểm của AB tớ có: \[SH \bot AB\]
Mặt khác
\[\begin{array}{l}\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\AB = \left( {SAB} \right) \cap \left( {ABCD} \right)\end{array} \right.\\ \Rightarrow SH \bot \left( {ABCD} \right).\end{array}\]
Tam giác SAB đều cạnh 2a nên \[SH = a\sqrt 3 ,\]
\[HC = \sqrt {H{B^2} + B{C^2}} = a\sqrt 2 .\]
Do \[SH \bot \left( {ABCD} \right)\]\[ \Rightarrow \left( {\widehat {SB;\left( {ABCD} \right)}} \right) = \widehat {SBH} = 60^\circ \]
\[\left( {\widehat {SC;\left( {ABCD} \right)}} \right) = \widehat {SCH}\] và \[\tan \widehat {SCH} = \frac{{SH}}{{HC}} = \sqrt {\frac{3}{2}} .\]
b) Ta có:
\[\begin{array}{l}HI = \sqrt {H{B^2} + B{I^2}} \\ = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}.\end{array}\]
Mặt không giống \[\left( {\widehat {SI;\left( {ABCD} \right)}} \right) = \widehat {SIH}\] và \[\widehat {SIH} = \frac{{SH}}{{SI}} = a\sqrt 3 :\frac{{a\sqrt 5 }}{2} = \frac{{2\sqrt {15} }}{5}.\]
Ví dụ 3: Cho hình chóp S.ABCD, sở hữu lòng là nửa lục giác đều cạnh a, \[AD = 2a\]. sành \[SA \bot \left( {ABCD} \right)\] và đường thẳng liền mạch SB tạo nên với lòng một góc \[45^\circ .\]
a) Tính cosin góc tạo nên vày những cạnh SC, SD và mặt mày lòng (ABCD).
b) Gọi I là trung điểm của CD, tính tan góc tạo nên vày SI và mặt mày phẳng lặng (ABCD).
Lời giải
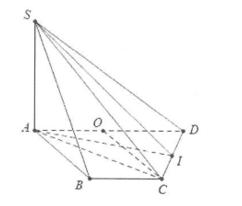
a) Gọi O là trung điểm của AD \[ \Rightarrow \] OABC là hình thoi cạnh a \[ \Rightarrow CO = a = \frac{1}{2}AD \Rightarrow \Delta ACD\] vuông bên trên C.
Do \[SA \bot \left( {ABCD} \right)\]\[ \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBA} = 45^\circ .\]
Do tê liệt \[SA = AB\tan 45^\circ = a.\]
\[\begin{array}{l}AC = \sqrt {A{D^2} - C{D^2}} = a\sqrt 3 \\ \Rightarrow \cos \widehat {\left( {SC;\left( {ABC} \right)} \right)} = \cos \widehat {SCA}\end{array}\]
\[\begin{array}{l} = \frac{{AC}}{{SC}} = \frac{{AC}}{{\sqrt {S{A^2} + A{C^2}} }}\\ = \frac{{a\sqrt 3 }}{{\sqrt {{a^2} + 3{a^2}} }} = \frac{{\sqrt 3 }}{2}.\end{array}\]
\[\begin{array}{l}\cos \left( {\widehat {SD;\left( {ABCD} \right)}} \right) = \cos \widehat {SDA}\\ = \frac{{AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{2}{{\sqrt 5 }}.\end{array}\]
b) Ta có:
\[\begin{array}{l}AI = \sqrt {A{C^2} + C{I^2}} \\ = \sqrt {3{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {13} }}{2}.\end{array}\]
Do đó
\[\begin{array}{l}\tan \widehat {\left( {SI;\left( {ABCD} \right)} \right)} = \tan \widehat {SIA}\\ = \frac{{SA}}{{AI}} = \frac{2}{{\sqrt {13} }}.\end{array}\]
Dạng 2: Góc thân thiết cạnh mặt mày và mặt mày phẳng lặng chứa chấp đàng cao

Tìm góc thân thiết cạnh mặt mày SB và mặt mày phẳng lặng (SHA) với \[\left( {SHA} \right) \bot \left( {ABH} \right).\]
Dựng \[BK \bot AH\], sở hữu \[BK \bot SH \Rightarrow BK \bot \left( {SHA} \right).\]
Suy đi ra K là hình chiếu vuông góc của B bên trên mặt mày phẳng lặng (SAH).
Vậy \[\widehat {\left( {SB;\left( {SAH} \right)} \right)} = \widehat {\left( {SB;SK} \right)} = \widehat {BSK}.\]
Ví dụ 1: Cho hình chóp S.ABCD sở hữu lòng là hình chữ nhật sở hữu \[AB = a,AD = a\sqrt 3 ,SA \bot \left( {ABCD} \right).\]
Biết SC tạo nên với lòng một góc \[60^\circ \]. Tính cosin góc tạo nên bởi:
a) SC và mặt mày phẳng lặng (SAB); SC và mặt mày phẳng lặng (SAD).
b) SD và mặt mày phẳng lặng (SAC).
Lời giải
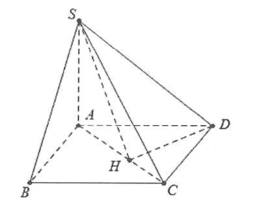
Do \[SA \bot \left( {ABCD} \right)\]\[ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\]
Lại có:
\[\begin{array}{l}AC = \sqrt {A{B^2} + A{D^2}} = 2a\\ \Rightarrow SA = AC\tan 60^\circ = 2a\sqrt 3 .\end{array}\]
Khi tê liệt \[\left\{ \begin{array}{l}SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt {13} \\SD = \sqrt {S{A^2} + A{D^2}} = a\sqrt {15} \\SC = \sqrt {S{A^2} + A{C^2}} = 4a.\end{array} \right.\]
Do \[\left\{ \begin{array}{l}CB \bot SA\\CB \bot AB\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)\]\[ \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {CSB}.\]
Mặt không giống \[\cos \widehat {CSB} = \frac{{SB}}{{SC}} = \frac{{\sqrt {13} }}{4}.\]
Tương tự động \[CD \bot \left( {SAD} \right) \Rightarrow \widehat {\left( {SC;\left( {SAD} \right)} \right)} = \widehat {CSD}\] và \[\cos \widehat {SCD} = \frac{{SD}}{{SC}} = \frac{{\sqrt {15} }}{4}.\]
Ví dụ 2: Cho hình chóp S.ABCD sở hữu lòng là hình thoi tâm O cạnh a, \[BD = a\sqrt 3 ,SA \bot \left( {ABCD} \right).\]
Biết SC tạo nên với lòng một góc \[60^\circ \]. Tính tan góc tạo nên bởi:
a) SC và mặt mày phẳng lặng (SAB).
b) SD và mặt mày phẳng lặng (SAC).
Lời giải
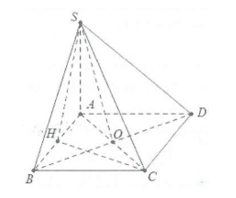
a) Ta có: \[AC \bot BD\] bên trên O. Khi tê liệt \[OA = OC,OB = OD.\]
Xét tam giác vuông OAB tớ có: \[\sin \widehat {OAB} = \frac{{OB}}{{AB}} = \frac{{\sqrt 3 }}{2}\]
\[ \Rightarrow \widehat {OAB} = 60^\circ \Rightarrow \Delta ABC\] đều cạnh a.
Mặt không giống
\[\begin{array}{l}SA \bot \left( {ABCD} \right)\\ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\end{array}\]
Suy đi ra \[SA = AC\tan 60^\circ = a\sqrt 3 .\]
Dựng \[CH \bot AB \Rightarrow CH \bot \left( {SAB} \right)\]
\[ \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {CSH}.\]
Do \[\Delta ABC\] đều cạnh a nên H là trung điểm của AB.
Ta có: \[CH = \frac{{a\sqrt 3 }}{2} \Rightarrow \tan \widehat {CSH} = \frac{{CH}}{{SH}}\] nhập tê liệt \[SH = \sqrt {S{A^2} + A{H^2}} = \frac{{a\sqrt {13} }}{2}.\]
Do tê liệt \[\tan \widehat {CSH} = \frac{{\sqrt 3 }}{{\sqrt {13} }} = \frac{{\sqrt {39} }}{{13}}.\]
b) Ta có:
\[\left\{ \begin{array}{l}DO \bot AC\\DO \bot SA\end{array} \right. \Rightarrow \left( {\widehat {SD;\left( {SAC} \right)}} \right) = \widehat {DSO}\] và \[\tan \widehat {DSO} = \frac{{OD}}{{SO}}.\]
Trong đó
\[\begin{array}{l}OD = \frac{{a\sqrt 3 }}{2};\\SO = \sqrt {S{A^2} + O{A^2}} = \frac{{a\sqrt {13} }}{2}\\ \Rightarrow \tan \widehat {DSO} = \frac{{\sqrt {39} }}{{13}}.\end{array}\]
Ví dụ 3: Cho hình chóp S.ABCD sở hữu lòng là hình chữ nhật ABCD, hình chiếu vuông góc của đỉnh S lên trên bề mặt lòng là vấn đề H nằm trong cạnh AB sao mang lại \[\overrightarrow {HB} = - 2\overrightarrow {HA} \]. Biết \[AB = 3,AD = 6\] và \[SH = 2\]. Tính tan góc tạo nên bởi:
a) SA và mặt mày phẳng lặng (SHD).
b) SB và mặt mày phẳng lặng (SHC).
Lời giải
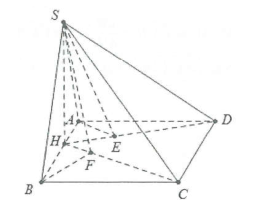
a) Ta có:
\[\begin{array}{l}AH = 1,HB = 2\\ \Rightarrow \left\{ \begin{array}{l}SA = \sqrt {S{H^2} + A{H^2}} = \sqrt 5 \\SB = \sqrt {S{H^2} + H{B^2}} = 2\sqrt 2 \end{array} \right.\end{array}\]
Dựng
\[\begin{array}{l}AE \bot DH \Rightarrow AE \bot \left( {SHD} \right)\\ \Rightarrow \widehat {\left( {SA;\left( {SHD} \right)} \right)}{\rm{ = }}\widehat {{\rm{ASE}}}\end{array}\]
Mặt không giống \[AE = \frac{{AH.AD}}{{\sqrt {A{H^2} + A{D^2}} }} = \frac{6}{{\sqrt {37} }}\]
Suy đi ra \[\tan \widehat {{\rm{ASE}}} = \frac{{AE}}{{SA}} = \frac{6}{{\sqrt {185} }}.\]
b) Dựng \[BF \bot HC \Rightarrow BF \bot \left( {SHC} \right).\]
Khi tê liệt \[\widehat {\left( {SB;\left( {SHC} \right)} \right)}{\rm{ = }}\widehat {BSF}\], \[BF = \frac{{BH.BC}}{{\sqrt {B{H^2} + B{C^2}} }} = \frac{{3\sqrt {10} }}{5}.\]
Ta có: \[\tan \widehat {\left( {SB;\left( {SHC} \right)} \right)} = \tan \widehat {BSF} = \frac{{BF}}{{SB}} = \frac{{3\sqrt 5 }}{{10}}.\]
Ví dụ 4: Cho hình lăng trụ \[ABCD.A'B'C'D'\] sở hữu lòng ABCD là hình chữ nhật có\[AB = 2a,AD = 2a\sqrt 3 \], hình chiếu vuông góc của \[A'\] lên trên bề mặt phẳng lặng (ABCD) trùng với tâm O của hình chữ nhật ABCD, biết cạnh mặt mày \[AA'\] tạo nên với lòng một góc \[60^\circ \]. Tính cosin góc tạo nên với \[A'C\] và mặt mày phẳng lặng \[\left( {A'BD} \right).\]
Lời giải
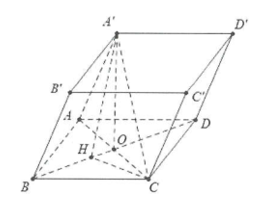
Ta có:
\[\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = 4a\\ \Rightarrow OA = 2a = OC.\end{array}\]
Do \[A'O \bot \left( {ABCD} \right)\]\[ \Rightarrow \widehat {\left( {A'O;\left( {ABCD} \right)} \right)} = \widehat {A'AO} = 60^\circ .\]
\[ \Rightarrow A'O = OA\tan 60^\circ = 2a\sqrt 3 \]
Dựng \[CH \bot BD \Rightarrow CH \bot \left( {A'BD} \right)\]
\[ \Rightarrow \widehat {\left( {A'C;\left( {A'BD} \right)} \right)} = \widehat {CA'H}.\]
Ta có: \[CH = \frac{{BC.CD}}{{\sqrt {B{C^2} + C{D^2}} }} = a\sqrt 3 .\]
\[A'C = \sqrt {O{{A'}^2} + O{C^2}} = \sqrt {12{a^2} + 4{a^2}} = 4a.\]
Suy ra
\[\begin{array}{l}\cos \widehat {CA'H} = \frac{{A'H}}{{A'C}} = \frac{{\sqrt {A'{C^2} - H{C^2}} }}{{A'C}}\\ = \frac{{\sqrt {16{a^2} - 3{a^2}} }}{{4a}} = \frac{{\sqrt {13} }}{4}.\end{array}\]
Ví dụ 5: Cho hình lăng trụ đứng \[ABC.A'B'C'\] sở hữu lòng là tam giác đều cạnh a. Tính góc tạo nên vày \[A'C\] và mặt mày phẳng lặng \[\left( {ABB'A'} \right)\] biết \[AA' = \frac{{a\sqrt 2 }}{2}.\]
Lời giải

Dựng \[CH \bot AB \Rightarrow CH = \frac{{a\sqrt 3 }}{2}.\]
Do
\[\begin{array}{l}\left\{ \begin{array}{l}CH \bot AB\\CH \bot AA'\end{array} \right. \Rightarrow CH \bot \left( {ABB'A'} \right)\\ \Rightarrow \widehat {\left( {A'C;\left( {ABB'A'} \right)} \right)} = \widehat {CA'H}.\end{array}\]
Lại có: \[A'H = \sqrt {A{{A'}^2} + A{H^2}} = \sqrt {\frac{{{a^2}}}{2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{4}.\]
Do tê liệt \[\tan \widehat {CA'H} = \frac{{CH}}{{A'H}} = 1 \Rightarrow \widehat {CA'H} = 45^\circ .\]
Vậy \[\widehat {\left( {A'C;\left( {ABB'A'} \right)} \right)} = \widehat {CA'H} = 45^\circ .\]
Xem thêm: 50+ kiểu tóc ngắn đẹp cho nữ xu hướng HOT trend 2024 trẻ trung, cá tính
Dạng 3: Góc thân thiết đàng cao và mặt mày bên
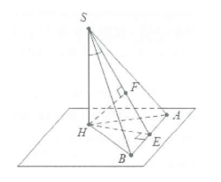
Tìm góc thân thiết đàng cao SH và mặt mày phẳng lặng (SAB).
Dựng \[HE \bot AB,HF \bot SE.\]
Ta có: \[AB \bot SH \Rightarrow AB \bot \left( {SHE} \right) \Rightarrow AB \bot HF.\]
Mặt không giống \[HF \bot SE \Rightarrow HF \bot \left( {SAB} \right) \Rightarrow F\] là hình chiếu vuông góc của H bên trên mặt mày phẳng lặng (SAB).
Vậy \[\widehat {\left( {SH;SAB} \right)} = \widehat {\left( {HF;SF} \right)} = \widehat {HSF}.\]
Ví dụ 1: Cho hình chóp S.ABC, sở hữu lòng ABC là tam giác đều cạnh 2a. Cạnh mặt mày \[SA = a\sqrt 3 \] và vuông góc với lòng. Tính góc thân thiết SA và mặt mày phẳng lặng (SBC).
Lời giải
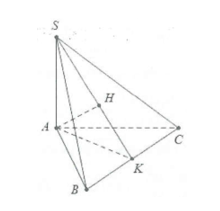
Từ A kẻ AK vuông góc với BC bên trên K.
Ta sở hữu : \[SA \bot BC\] và \[AK \bot BC \Rightarrow BC \bot \left( {SAK} \right).\]
Kẻ \[AH \bot SK,H \in SK\]. Mà \[BC \bot AH.\]
Suy đi ra \[AH \bot \left( {SBC} \right) \Rightarrow \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASH} = \widehat {ASK}.\]
Tam giác SAK vuông bên trên A, sở hữu \[SA = AK = a\sqrt 3 .\]
\[ \Rightarrow \] tam giác SAK vuông cân nặng bên trên A nên \[ASK = 45^\circ .\]
Vậy \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = 45^\circ .\]
Ví dụ 2: Cho hình chóp S.ABCD sở hữu lòng là hình chữ nhật sở hữu \[AB = a,AD = 2a,SA = 2a\] và \[SA \bot \left( {ABCD} \right)\]. Tính tan góc thân thiết SA và những mặt mày phẳng lặng (SBC), (SBD) và (SCD).
Lời giải
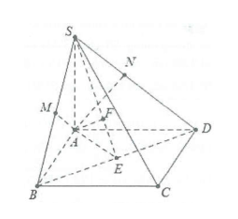
Do \[\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right).\]
Dựng \[AM \bot SB \Rightarrow AM \bot \left( {SBC} \right)\]
\[ \Rightarrow \] M là hình chiếu vuông góc của A bên trên (SBC).
Khi đó: \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASM} = \widehat {ASB} = \alpha .\]
Do tê liệt \[\tan \alpha = \frac{{AB}}{{SA}} = \frac{1}{2}.\]
Tương tự động tớ có: \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASD} = \beta \] và \[\tan \beta = \frac{{AD}}{{SA}} = 1.\]
Dựng \[AE \bot BD,AF \bot SE\] tớ có:
\[\left\{ \begin{array}{l}BD \bot AE\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAE} \right) \Rightarrow BD \bot AF.\]
Mặt không giống
\[\begin{array}{l}AF \bot SE \Rightarrow AF \bot \left( {SBD} \right)\\ \Rightarrow \widehat {\left( {SA;\left( {SBD} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\end{array}\]
Khi tê liệt \[\tan \widehat {ASE} = \frac{{AE}}{{SA}}\], nhập đó
\[\begin{array}{l}AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{2a}}{{\sqrt 5 }}\\ \Rightarrow \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{1}{{\sqrt 5 }}.\end{array}\]
Ví dụ 3: Cho hình chóp S.ABCD sở hữu lòng là hình thang vuông bên trên A và B sở hữu \[AD = 2AB = 2CD = 2a\] và \[SA \bot \left( {ABCD} \right)\]. sành rằng SC tạo nên với lòng một góc \[60^\circ \]. Tính tan góc thân thiết SA và những mặt mày phẳng lặng (SBC), (SCD) và (SBD).
Lời giải
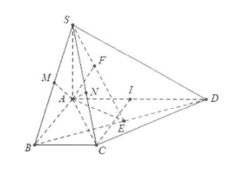
Ta có: \[AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \]
Do \[SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\]
Suy đi ra \[SA = AC\tan 60^\circ = a\sqrt 6 .\]
Dựng \[AM \bot SB\] sở hữu \[\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot AM.\]
Do tê liệt \[AM \bot \left( {SBC} \right) \Rightarrow \] M là hình chiếu của A bên trên mặt mày phẳng lặng (SBC).
Suy đi ra \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASM} = \widehat {ASB}.\]
Ta có: \[\tan \widehat {ASB} = \frac{{AB}}{{SA}} = \frac{a}{{a\sqrt 6 }} = \frac{1}{{\sqrt 6 }}.\]
Gọi I là trung điểm của AD \[ \Rightarrow \] ABCI là hình vuông vắn cạnh a \[ \Rightarrow CI = \frac{{AD}}{2} = a \Rightarrow \Delta ACD\] vuông bên trên C.
Khi tê liệt \[\left\{ \begin{array}{l}CD \bot SA\\CD \bot AC\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\]
Dựng \[AN \bot SC \Rightarrow \widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASN} = \widehat {ASC}.\]
Ta có: \[\tan \widehat {ASC} = \frac{{AC}}{{SA}} = \frac{{a\sqrt 2 }}{{a\sqrt 6 }} = \frac{1}{{\sqrt 3 }}.\]
Dựng \[\left\{ \begin{array}{l}AE \bot BD\\AF \bot SE\end{array} \right. \Rightarrow \widehat {\left( {SA;\left( {SBD} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\]
Mặt không giống
\[\begin{array}{l}AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{2a}}{{\sqrt 5 }}\\ \Rightarrow \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{{\sqrt {30} }}{{15}}.\end{array}\]
Ví dụ 4: Cho hình chóp S.ABCD, sở hữu lòng là nửa lục giác đều cạnh a, \[AD = 2a\]. sành \[SA \bot \left( {ABCD} \right)\] và đường thẳng liền mạch SB tạo nên với lòng một góc 60°.
a) Tính tan góc tạo nên vày SA và (SBC).
b) Tính góc tạo nên vày SA và (SCD).
Lời giải
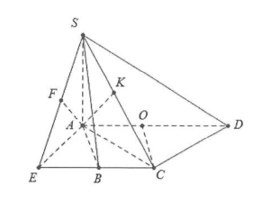
a) Gọi O là trung điểm của AD \[ \Rightarrow \] OABC là hình thoi cạnh a \[ \Rightarrow CO = a = \frac{1}{2}AD \Rightarrow \Delta ACD\] vuông bên trên C.
Do \[SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBA} = 60^\circ .\]
\[ \Rightarrow SA = AB\tan 60^\circ = a\sqrt 3 \], \[AC = \sqrt {A{D^2} - C{D^2}} = a\sqrt 3 .\]
Dựng \[AE \bot BC\], \[AF \bot SE\]
\[ \Rightarrow \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\]
Do \[\widehat {ABE} = 120^\circ \Rightarrow \widehat {ABE} = 60^\circ .\]
Mặt không giống \[AE = AB\sin \widehat {ABE} = AB\sin 60^\circ = \frac{{a\sqrt 3 }}{2}.\]
Suy đi ra \[\tan \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{1}{2}.\]
b) Do \[\left\{ \begin{array}{l}CD \bot SA\\CD \bot AC\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\]
Dựng \[AK \bot SC \Rightarrow AK \bot \left( {SCD} \right)\]
Khi tê liệt \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASK} = \widehat {ASC} = \varphi .\]
Ta có: \[\tan \varphi = \frac{{AC}}{{SA}} = \frac{{a\sqrt 3 }}{{a\sqrt 3 }} = 1 \Rightarrow \varphi = 45^\circ .\]
Vậy \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = 45^\circ .\]
Ví dụ 5: Cho hình lăng trụ \[ABC.A'B'C'\] sở hữu lòng là tam giác đều cạnh a, hình chiếu vuông góc của \[B'\] lên trên bề mặt phẳng lặng lòng trùng với trung điểm H của cạnh AB, đàng cao \[B'H = \frac{{3a}}{4}\]. Tính cosin góc thân thiết đường thẳng liền mạch \[B'H\] và mặt mày phẳng lặng \[\left( {BCC'B'} \right)\].
Lời giải
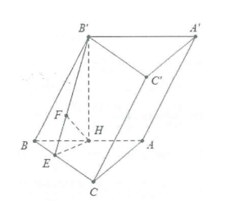
Dựng \[HE \bot BC,HF \bot B'E\] tớ có:
\[\left\{ \begin{array}{l}BC \bot B'H\\BC \bot HE\end{array} \right.\] suy ra
\[\begin{array}{l}BC \bot HF \Rightarrow HF \bot \left( {B'BCC'} \right)\\ \Rightarrow \widehat {\left( {B'H;\left( {BCC'B'} \right)} \right)}\end{array}\]
\[ = \widehat {HB'F} = \widehat {HB'E}.\]
Ta có: \[HE = HB\sin \widehat {HBE} = \frac{a}{2}\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\]
Do tê liệt \[\cos \widehat {HB'E} = \frac{{B'H}}{{B'E}} = \frac{{B'H}}{{\sqrt {B'{H^2} + H{E^2}} }} = \frac{{\sqrt 3 }}{2}.\]
Dạng 4: Góc thân thiết cạnh mặt mày và mặt mày bên
Tính góc thân thiết cạnh mặt mày SC và mặt mày phẳng lặng (SAB). Đặt \[\widehat {\left( {SC;\left( {SAB} \right)} \right)} = \varphi \left( {0^\circ \le \varphi \le 90^\circ } \right).\]
Ta sở hữu công thức: \[\sin \varphi = \frac{{d\left( {C;\left( {SAB} \right)} \right)}}{{SC}}.\]
Từ tê liệt suy đi ra những độ quý hiếm \[\cos \varphi \] hoặc \[\tan \varphi \] nếu đề bài bác đòi hỏi.
Ví dụ 1: Cho hình chóp S.ABCD sở hữu lòng ABCD là hình chữ nhật sở hữu \[AD = 2a,AB = a\sqrt 2 \]. Tam giác SAD cân nặng bên trên S và nằm trong mặt mày phẳng lặng vuông góc với lòng. Đường trực tiếp SB tạo nên với lòng một góc \[30^\circ \]. Tính sin góc tạo nên bởi:
a) SA và mặt mày phẳng lặng (SBC).
b) SD và mặt mày phẳng lặng (SAC).
Lời giải
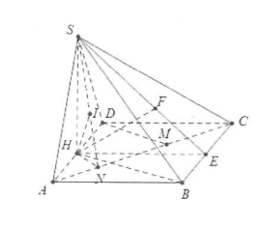
Gọi H là trung điểm của AD tớ có: \[SH \bot AD\]
Lại có: \[\left( {SAD} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right).\]
Ta có: \[HA = a;HB = \sqrt {H{A^2} + A{B^2}} = a\sqrt 3 \]
Do \[SH \bot \left( {ABCD} \right)\]
\[ \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBH} = 30^\circ \]
Suy đi ra \[SH = HB\tan 30^\circ = a.\]
a) Do \[AD//BC \Rightarrow AD//\left( {SBC} \right).\]
Do vậy \[d\left( {A;\left( {SBC} \right)} \right) = d\left( {H;\left( {SBC} \right)} \right).\]
Dựng \[\left\{ \begin{array}{l}HE \bot BC\\HF \bot SE\end{array} \right.\] tacó: \[BC \bot HF\] kể từ tê liệt suy đi ra \[HF \bot \left( {SBC} \right)\]
\[ \Rightarrow d\left( {H;\left( {SBC} \right)} \right) = HF = d\left( {A;\left( {SBC} \right)} \right).\]
Ta có: \[SA = \sqrt {S{H^2} + S{A^2}} = a\sqrt 2 = SD.\]
Mặt khác:
\[\begin{array}{l}\frac{1}{{H{F^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{E^2}}} \Rightarrow HF = \frac{{a\sqrt 6 }}{3}\\ \Rightarrow \sin \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{SA}} = \frac{{\sqrt 3 }}{3}.\end{array}\]
b) Dựng \[HN \bot AC \Rightarrow AC \bot \left( {SHN} \right)\]
Dựng \[HI \bot SN \Rightarrow HI \bot \left( {SAC} \right)\]
Do \[\frac{{DA}}{{HA}} = 2 = \frac{{d\left( {D;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}}\]
\[ \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right) = 2HI\]
Dựng \[DM \bot AC \Rightarrow DM = \frac{{2a\sqrt 2 }}{{\sqrt 6 }} \Rightarrow HN = \frac{a}{{\sqrt 3 }}\]
\[ \Rightarrow HI = \frac{{HN.SH}}{{\sqrt {H{N^2} + S{H^2}} }} = \frac{a}{2} \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = a.\]
Ta có: \[\sin \widehat {\left( {SD;\left( {SAC} \right)} \right)} = \frac{{d\left( {D;\left( {SAC} \right)} \right)}}{{SD}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\]
Ví dụ 2: Cho hình chóp S.ABCD sở hữu lòng là hình chữ nhật ABCD sở hữu \[AB = a\sqrt 3 ;AD = a\], tam giác SBD là tam giác vuông cân nặng đỉnh S và trực thuộc mặt mày phẳng lặng vuông góc với mặt mày phẳng lặng lòng. Tính sin góc tạo nên vày SA và mặt mày phẳng lặng (SBC).
Lời giải
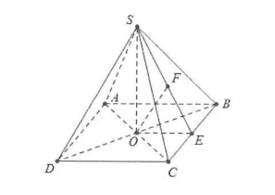
Gọi O là trung điểm của BD tớ có: \[SO \bot BC\] mặt không giống \[\left( {SBD} \right) \bot \left( {ABC} \right) \Rightarrow SO \bot \left( {ABC} \right)\]
Ta có: \[BD = \sqrt {A{B^2} + A{D^2}} = 2a \Rightarrow SO = \frac{1}{2}BD = a.\]
Dựng \[OE \bot BC,OF \bot SE \Rightarrow OF \bot \left( {SBC} \right).\]
\[d\left( {D;\left( {SBC} \right)} \right) = 2d\left( {O;\left( {SBC} \right)} \right) = 2HF\]
Ta có: \[HE = \frac{1}{2}AB = \frac{{a\sqrt 3 }}{2}\]
\[ \Rightarrow OF = \frac{{SH.OE}}{{\sqrt {S{H^2} + O{E^2}} }} = a\sqrt {\frac{3}{7}} = \frac{{a\sqrt {21} }}{7}\]
Suy đi ra \[d\left( {A;\left( {SBC} \right)} \right) = \frac{{2a\sqrt {21} }}{7}.\]
Mặt không giống \[SA = \sqrt {S{O^2} + O{A^2}} = a\sqrt 2 .\]
Do tê liệt \[\sin \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{SA}} = \frac{{\sqrt {42} }}{7}.\]
Ví dụ 3: Cho hình lăng trụ \[ABC.A'B'C'\] sở hữu lòng là tam giác vuông bên trên A với \[AB = a;AC = a\sqrt 3 \], hình chiếu vuông góc của \[A'\] lên trên bề mặt lòng trùng với trung điểm H của BC. sành \[A'H = a\sqrt 2 \]. Tính cosin góc tạo nên vày \[A'B\] với mặt mày phẳng lặng \[\left( {ACC'A'} \right)\].
Lời giải
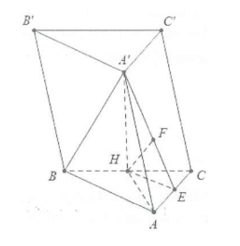
Dựng \[HE \bot AC\] và \[HF \bot A'E\]
Ta có: \[\left\{ \begin{array}{l}AC \bot A'H\\AC \bot HE\end{array} \right. \Rightarrow AC \bot HF \Rightarrow HF \bot \left( {AA'C} \right).\]
Khi tê liệt \[d\left( {H;\left( {A'AC} \right)} \right) = HF.\]
Lại sở hữu \[BC = 2HC\] nên \[d\left( {B;\left( {AA'C} \right)} \right) = 2d\left( {H;\left( {AA'C} \right)} \right).\]
Mặt không giống ME là đàng khoảng nhập tam giác ABC
nên \[ME = \frac{{AB}}{2} = \frac{a}{2}.\]
Khi đó: \[HF = \frac{{HE.A'M}}{{\sqrt {H{E^2} + A'{M^2}} }} = \frac{{a\sqrt 2 }}{3}\]
Suy đi ra \[d\left( {B;\left( {AA'C} \right)} \right) = \frac{{2a\sqrt 2 }}{3};BC = \sqrt {A{B^2} + A{C^2}} = 2a.\]
Xem thêm: Tuổi Giáp Thân 2004 mệnh gì? Hợp màu gì, hợp tuổi gì, hướng nào tốt? | Mytour
Lại sở hữu \[A'B = \sqrt {A'{H^2} + H{B^2}} = a\sqrt 3 .\]
Suy đi ra \[\sin \widehat {\left( {A'B;\left( {A'AC} \right)} \right)} = \sin \varphi = \frac{{d\left( {B;\left( {A'AC} \right)} \right)}}{{BA'}} = \frac{{2\sqrt 6 }}{9}\]
\[ \Rightarrow \cos \varphi = \sqrt {1 - {{\sin }^2}\varphi } = \frac{{\sqrt {57} }}{9}.\]













Bình luận